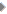लेखक: कॉन्स्टेन्स कामी और लिण्डा जोसेफ
अनुवाद: सुशील जोशी
प्राथमिक कक्षाओं में गणित
दूसरी कक्षा में पढ़ने वाले अधिकांश छात्र दो अंकों की संख्या का जोड़ सही कर लेते हैं। इसके लिए वे पहले इकाइयों को जोड़ते हैं:
गणित का पीरियड पूरा होने के बाद जब हमने इन बच्चों से अलग-अलग बात की, तो अधिकांश ने कहा कि 16 में 1 का मतलब ‘एक’ होता है। हमने कक्षा 1-3 के सैकड़ों बच्चों से बात की है, और उनके शिक्षकों को इस बात पर कभी यकीन नहीं होता कि उनके छात्रों को लगता है कि 16 में 1 का मतलब एक होता है। यहां हम बच्चों से अपनी बातचीत का ब्यौरा दे रहे हैं ताकि शिक्षक एक-दूसरे के छात्रों का परीक्षण इसी तरह कर सकें। (हमने ‘एक-दूसरे के छात्रों’ की बात इसलिए कही है क्योंकि अक्सर बच्चे उस उत्तर के बारे में सोचते हैं जिसकी उनके शिक्षक अपेक्षा करते हैं जब वही व्यक्ति पूछता है जिसने उन्हें पढ़ाया हो।)
बच्चों से साक्षात्कार जब बच्चा बातचीत के लिए अंदर आता है, तो साक्षात्कारकर्ता 3 x 5 इंच आकार का एक कार्ड उसे दिखाता है जिस पर ‘16’ लिखा है। जब बच्चा कहता है कि उस कार्ड पर ‘सोलह’ दर्शाया गया है, तब उसे 16 तीलियां गिनने को कहा जाता है। अब साक्षात्कारकर्ता 16 के 6 को पेन के पिछले हिस्से से गोले में घेरकर पूछता है, ‘‘इस भाग (6) का क्या मतलब है? क्या तुम मुझे तीली की मदद से बता सकते हो कि इस भाग (6) का क्या मतलब है?’’ पहली और दूसरी कक्षा के छात्रों को साक्षात्कार के इस पड़ाव पर कोई दिक्कत नहीं आती।
जब बच्चा बातचीत के लिए अंदर आता है, तो साक्षात्कारकर्ता 3 x 5 इंच आकार का एक कार्ड उसे दिखाता है जिस पर ‘16’ लिखा है। जब बच्चा कहता है कि उस कार्ड पर ‘सोलह’ दर्शाया गया है, तब उसे 16 तीलियां गिनने को कहा जाता है। अब साक्षात्कारकर्ता 16 के 6 को पेन के पिछले हिस्से से गोले में घेरकर पूछता है, ‘‘इस भाग (6) का क्या मतलब है? क्या तुम मुझे तीली की मदद से बता सकते हो कि इस भाग (6) का क्या मतलब है?’’ पहली और दूसरी कक्षा के छात्रों को साक्षात्कार के इस पड़ाव पर कोई दिक्कत नहीं आती।
इसके बाद साक्षात्कारकर्ता 16 के 1 को घेरकर पूछता है, “यह भाग (1) कितना है? क्या तुम तीलियों की मदद से बता सकते हो कि इस भाग (1) का क्या मतलब है?’’ यहां शब्द ‘इस भाग’ के इस्तेमाल पर गौर कीजिए। किसी अन्य शब्द का उपयोग न करें। पहली व दूसरी कक्षा के लगभग सारे छात्र जवाब के रूप में 1 ही तीली दिखाते हैं जबकि उन्हें स्थानीय मान को लेकर घंटों सिखाया गया है।
साक्षात्कारकर्ता आगे बढ़ता है: ‘‘तुमने मुझे इस संख्या (कार्ड पर 16 को घेरते हुए) के लिए ये सारी तीलियां दिखाईं (सोलह तीलियों की ओर इशारा करते हुए) और इस भाग (कार्ड पर 6 को घेरते हुए) के लिए ये तीली दिखाई (तीली में से छ: को घेरते हुए) और इस भाग (कार्ड पर 1 को घेरते हुए) के लिए यह तीली दिखाई (एक तीली को घेरते हुए)। बाकी तीलियां (उन 9 या 10 तीलियों को घेरते हुए जिनका उपयोग कार्ड के दो हिस्सों को दर्शाने के लिए नहीं किया गया है) का क्या हुआ? क्या यह ठीक है या कुछ गड़बड़ है?’’ कुछ बच्चों का जवाब होता है कि कुछ गड़बड़ है मगर अधिकांश बच्चे कहते हैं कि उन्हें अपनी बात में कुछ भी गड़बड़ नहीं लगता।
आमतौर पर देखा गया है कि पहली कक्षा के छात्रों में से यह कहने वाले शून्य प्रतिशत होते हैं कि 1 का मतलब दस है जबकि तीसरी कक्षा के बच्चों में से 33 प्रतिशत और चौथी कक्षा के बच्चों में 50 प्रतिशत ऐसा कहते हैं। अलबत्ता यह बताते हुए कि 1 का मतलब दस होता है, बच्चे उन छ: तीलियों को भी शामिल कर लेते हैं जो उन्होंने 6 का मतलब बताते हुए दर्शाई थीं।
प्राथमिक कक्षाओं के बच्चे स्थानीय मान क्यों नहीं समझते? इस सवाल का जवाब पेचीदा है। ज़्यादा आसान यह होगा कि पहले दूसरी कक्षा के छात्रों को स्थानीय मान व दो अंकों की संख्याओं का जोड़ सिखाने का एक नया तरीका देख लिया जाए, जो ज़्यां पियाजे के सिद्धांत पर आधारित है। इस तरीके का विकास अलाबामा में बर्मिंघम के निकट स्थित हॉल केन्ट स्कूल में किया गया है। इसकी मदद से दूसरी कक्षा के बच्चों में स्थानीय मान की समझ पारंपरिक पाठ्य पुस्तक विधि की अपेक्षा कहीं बेहतर विकसित हुई। 1987 के स्कूल सत्र के अंत में 66 प्रतिशत बच्चों ने कहा कि 16 में 1 का मतलब 10 है और 74 प्रतिशत ने 54 में 5 का मतलब 50 बताया। ये प्रतिशत उन नतीजों से बेहतर हैं जो पारंपरिक शिक्षण के बाद आमतौर पर चौथी कक्षा के अंत में मिलते हैं। (गौरतलब है कि शिक्षण में इस सवाल को शामिल नहीं किया गया था और बच्चों से 10-10 चीज़ों के समूह बनाने को कभी नहीं कहा गया था। दूसरी कक्षा के इन छात्रों की पूरी गणित शिक्षा किंडरगार्टन और पहली कक्षा में खेलों तथा दूसरी कक्षा में खेलों तथा चर्चाओं पर आधारित थी। इसमें पाठ्यपुस्तकों या कार्यपुस्तिकाओं का बिल्कुल भी उपयोग नहीं किया गया था।)
स्थानीय मान और दो अंकों का जोड़ सिखाने का एक तरीका
पियाजे के सिद्धांत पर आधारित सिखाने के हमारे तरीके का मूल यह है कि बच्चों की कुदरती सोच को बढ़ावा दिया जाए और उन्हें दृष्टिकोणों का आदान-प्रदान करने के लिए प्रेरित किया जाए। मगर पहले दो बातें बताना मुनासिब होगा।
पहली बात यह है कि हमारे दूसरी कक्षा के छात्रों को पहली कक्षा में स्थानीय मान और दो अंकों का जोड़ कदापि नहीं सिखाया गया था। शोध से पता चलता है कि इस बात की संभावना बहुत कम है कि पहली कक्षा के बच्चे स्थानीय मान समझ पाएंगे। पहली कक्षा के छात्र ‘16’ को सोलह इकाइयों के रूप में देखते हैं (1 दहाई और 6 इकाई के रूप में नहीं)।
दूसरी बात यह है कि हमने जोड़ और किसी अन्य संक्रिया से स्वतंत्र स्थानीय मान सिखाने की कोई कोशिश नहीं की थी। हमने तीलियों जैसी चीज़ों की 10-10 की गठरियां बनाने की कोशिश कभी नहीं की और न ही बच्चों से कहा कि वे चित्रों पर घेरे खींचकर बताएं कि उनमें कितनी इकाइयां और कितनी दहाइयां दर्शाई गई हैं। इसका कारण थोड़ी देर में स्पष्ट होगा।
हम मैडेल से काफी प्रभावित थे जिन्होंने बताया है कि यदि बच्चों को दो अंकों के जोड़ उनके स्वाभाविक तरीके से करने दिए जाएं, तो ‘वे सभी बाएं से दाएं आगे बढ़ते हैं।’ जैसे एक उदाहरण के बारे में उन्होंने बताया था कि ऐसे सवाल में, बगैर अपवाद के, 7-8 वर्ष के बच्चे पहले दहाइयों की गणना करते हैं। बारीकियों में अंतर हो सकते हैं:
क - कुछ बच्चे इकाई को देखने से पहले ही दहाई के स्तंभ में 7 लिख लेते हैं। ये बच्चे बाद में लौटकर इसे मिटाते हैं।
ख - अन्य बच्चे 3 व 4 का जोड़ 7 कर लेने के बाद इसे लिखने से पहले इकाई के स्तंभ को देख लेते हैं कि कहीं उसमें एक और दहाई तो नहीं है।
ग - बहुत ही कम नफीस छात्र होते हैं जो पहले इकाई पर गौर करते हैं। वे यह देख लेते हैं (अक्सर अनुमान से) कि इकाई के स्तंभ में 10 से ज़्यादा इकाइयां हैं, फिर वे दहाई के स्तंभ पर आते हैं और वहां 8 लिखकर इकाई के स्तंभ पर लौटते हैं और गणना का अंतिम हिस्सा कर डालते हैं।
आखिरी वाली प्रक्रिया (ग) वह प्रक्रिया है जिसमें बच्चे मानक दाएं-से-बाएं वाले तरीके के सबसे नज़दीक आते हैं। यहां तक कि तीन व चार अंकों के जोड़ में भी, जहां दाएं-से-बाएं वाला तरीका ज़्यादा कारगर नज़र आता है, बच्चे बाकायदा दूसरी दिशा से (बाएं-से-दाएं) ही आगे बढ़ते हैं। मैडेल ने 10-आधार के गुटकों का उपयोग किया था मगर हमने बोर्ड पर सवाल लिखकर बच्चों के बीच विचारों के आदान-प्रदान का तरीका अपनाया। इसका कारण भी जल्दी ही स्पष्ट हो जाएगा। शिक्षक एक के बाद एक सवाल बोर्ड पर लिखते हैं। जैसे:
उत्तर पता कर लेने पर बच्चे हाथ उठाते हैं। पूरी कक्षा एक साथ काम कर सकती है या शिक्षक एक छोटी टोली के साथ काम कर सकते हैं।
हम बच्चों को दो अंकों का जोड़ करने का कोई तरीका नहीं सिखाते बल्कि उन्हें कई अलग-अलग तरीके गढ़ने को प्रेरित करते हैं।
जब अधिकांश बच्चों के हाथ उठ जाते हैं, तब शिक्षक एक-एक बच्चे को बुलाते हैं और उनके द्वारा दिए गए सारे उत्तर लिख देते हैं। इस बात की सावधानी रखी जाती है कि किसी उत्तर को गलत या सही न बताया जाए। फिर शिक्षक हरेक उत्तर की व्याख्या या बच्चे द्वारा रचा गया तरीका पूछते हैं। जैसे एक बच्ची शायद कहे, ‘मैंने 7 में से 2 लेकर 10 बनाया।’ तो शिक्षक लिखेंगे 2, इस तरह
जैसे-जैसे बच्ची बोलती है, शिक्षक फिर 8 के आगे लिखते हैं ‘+2 = 10’, और 7-2 के आगे लिखते हैं ‘= 5’। कभी-कभी शिक्षक 8 को काटकर उसके आगे ‘10’ तथा 7 को काटकर उसके आगे ‘5’ लिख देते हैं।
अगला बच्चा शायद कहे, ‘सात धन सात चौदह होते हैं; तो एक और जोड़ने से पंद्रह होगा।’ शिक्षक पूछते जाते हैं कि क्या किसी के पास और कोई तरीका है, जब तक कि कोई अलग तरीका नहीं सोच पाता।
इस तरह से बच्चों को तमाम किस्म के तरीके खोजने और एक-दूसरे से सहमत-असहमत होने को प्रेरित किया जाता है। यदि विभिन्न तरीके ठीक लगते हैं, तो हम यह नहीं कहते कि कोई तरीका दूसरे से बेहतर है। बच्चे को वह तरीका अपनाने की छूट दी जाती है जो उसे सबसे अच्छा लगे।
यदि सवाल इस तरह का हो, तो हमारे सारे बच्चे दहाई से शुरु करना पसंद करते हैं, जैसा कि मैडेल ने कहा है। अधिकांश बच्चे कुछ इस तरह की बात कहते हैं:
‘तीस और चालीस सत्तर होते हैं।’ (शिक्षक बोर्ड पर बाजू में या कहीं भी याद रखने के लिए ‘70’ लिख देता है।)
‘छ: और छ: बारह होते हैं।’ (शिक्षक बाजू में ‘12’ भी लिख देता है।)
‘बारह में से दस लेकर उसे सत्तर के साथ रख दो, वह अस्सी हो जाएगा।’ (शिक्षक 12 का 1 मिटा देता है और 70 के 7 को मिटाकर 8 कर देता है।)
‘दो और जोड़कर बयासी हो जाएंगे।’ (शिक्षक सवाल के नीचे 82 लिख देता है।)
कुछ बच्चे यह कहते हैं:
‘तीस और चालीस सत्तर होते हैं।’ (शिक्षक बोर्ड पर बाजू में ‘70’ लिख देता है।)
‘‘छ: और चार मिलकर एक दस और हो गया; तो यह अस्सी हो गया।’’ (शिक्षक 70 के सात को मिटाकर 8 कर देता है।)
‘और दो जोड़कर बयासी हुए।’ (शिक्षक 80 के 0 को मिटाकर 2 कर देता है।)
जब कोई बच्ची कहती है कि ‘तीन और चार सत्तर होते हैं’ तो बच्चे या तो हाथ उठाते हैं या चिल्ला पड़ते हैं, ‘असहमत हैं’। यह इस बात पर निर्भर है कि उन्होंने क्या नियम तय किया है कि चिल्लाएंगे या हाथ उठाएंगे। अलबत्ता, शुरु में तो शिक्षक को ही कहना पड़ता है कि ‘मेरे ख्याल से तो तीन और चार सात होते हैं, तुम्हारे सत्तर कैसे आए?’ (शिक्षक को यह सावधानी रखनी पड़ती है कि वह सर्वज्ञाता अधिकारी नहीं है जो गलत-सही के फैसले करता है। वह सिर्फ सहमति या असहमति जताता है और एक भिन्न मत बराबरी से रखता है।)
पारंपरिक शिक्षा से फर्क
स्थानीय मान व दो अंकों की संख्याओं के जोड़ सिखाने का हमारा तरीका पारंपरिक शिक्षण से तीन मायनों में अलग है। पहले अंतर बता दें फिर उनकी व्याख्या करेंगे।
क- हम बच्चों को स्थानीय मान, दो अंकों के जोड़ की तैयारी के रूप में, एक अलग गतिविधि के रूप में नहीं सिखाते।
ख- हम दो अंकों के जोड़ का कोई तरीका या सूत्रविधि (एल्गोरिद्म) नहीं सिखाते, बल्कि हम बच्चों को कई अलग-अलग तरीके गढ़ने के लिए प्रेरित करते हैं।
ग- हम बच्चों को एक-दूसरे से सहमत या असहमत होने तथा जो तरीका उन्हें ठीक लगे वह अपनाने के लिए प्रेरित करते हैं।
‘दहाई और इकाई’ की समझ के लिए ज़रूरी होता है कि अपने दिमाग में दो प्रणालियां निर्मित की जाएं जो एक साथ काम करती हैं: एक इकाई प्रणाली और एक दहाई प्रणाली। ये प्रणालियां हर बच्चे को स्वयं अपनी मानसिक गतिविधि द्वारा अपने अंदर से बनाना पड़ती हैं। चित्र-2 में एक बच्ची द्वारा पहले बनाई गई इकाई प्रणाली से मानसिक रूप से रचित दहाई प्रणाली दर्शाई गई है।
इकाई प्रणाली बच्ची द्वारा रचित दो तरह के अंतर्सम्बंधों का संश्लेषण है: क्रमिकता और सोपानबद्ध समावेश। चित्र-2 में क्रमिकता का सम्बंध बत्तीस घटकों को जोड़ने वाली रेखा से दर्शाया गया है, और सोपानबद्ध समावेश को अण्डाकार रचनाओं से दर्शाया गया है जिनमें क्रमश: एक का दो में, दो का तीन में सोपानबद्ध समावेश दिखता है। इकाइयों की यह प्रणाली प्राकृत संख्याएं हैं जिसे अधिकांश बच्चे कक्षा 1 तक स्वयं निर्मित कर लेते हैं।
चित्र-3 में सारी सीधी व वक्र रेखाएं वे अंतर्सम्बंध दर्शाती हैं, जो बच्चे अपने मन में निर्मित करते हैं और वस्तुओं पर आरोपित करते हैं। जिन अनुभव वादी-सम्बद्धतावादी (Empiricist-associationist) मान्यताओं पर पारंपरिक गणित शिक्षण टिका है, उनके विपरीत दरअसल बच्चों के दिमाग में किसी बाहरी स्रोत से अंतर्सम्बंध ठूंसे नहीं जा सकते। अंतर्सम्बंध तो बच्चों को अपनी मानसिक गतिविधि से निर्मित करना पड़ते हैं। इसलिए किसी बच्चे को चित्र दिखाने से उसे दहाई की प्रणाली को सीखने में कोई मदद नहीं मिलेगी। जो पाठक बच्चों द्वारा दहाई की प्रणाली के निर्माण के बारे में और जानना चाहते हैं, वे कृपया सी. कामी के अन्य लेख देखें।
दाएं-से-बाएं की विधि सिखाने से बच्चों की दहाई व इकाई सीखने की संभावना कुंठित होती है। वयस्क भी बत्तीस को ‘दो और तीस’ की बजाय ‘तीस और दो’ के रूप में ही समझते हैं। जब बच्चों को जोड़ने के अपने तरीके खोजने को प्रेरित किया जाता है, तब कोई आश्चर्य नहीं कि वे पहले दहाई और फिर इकाई को संभालते हैं।
पारंपरिक शिक्षण में बच्चों से कहा जाता है कि वे पहले इकाइयां जोड़ें और दूसरे स्तंभ के दोनों 3 को दहाई मानें। इसलिए वे यह कभी नहीं सोचते कि ये दो 3 वास्तव में ‘तीस और तीस’ हैं। और यही सोच तो उन्हें दहाई व इकाई का विचार निर्मित करने में मदद करेगा।
हम इस परंपरागत अर्थ में बच्चों को कुछ नहीं पढ़ाते कि उन्हें बताएं कि कोई चीज़ कैसे करना है। न ही हम सही उत्तरों की पुष्टि करने या गलत उत्तरों को सुधारने जैसा कुछ करते हैं। पियाजे के शोध व सिद्धांत ने सिद्ध कर दिया है कि बच्चों को संख्या या स्थानीय मान या संक्रियाएं बाहर से संप्रेषित नहीं की जा सकतीं। यदि बच्चों को मानक तरीकों का खुद के लिए पुन: आविष्कार करना है, तो उन्हें अपने अंदर से, अपने सोच के आधार पर स्वयं अपना तार्किक-गणितीय ज्ञान निर्मित करना होगा।
हमारे स्कूल में आने वाले मेहमान अक्सर पूछते हैं कि हम पहले वर्ष में शुरुआत कहां से करते हैं। मूलत: शिक्षक कोई सवाल बनाता है ताकि बच्चे उन चीज़ों का उपयोग कर सकें जो वे पहले से जानते हैं और नई परिस्थितियों से निपटने के तरीके बना सकें। उदाहरण के लिए, यदि वे
को (8 + 2) + 5 में बदल लेते हैं, तो शिक्षक बोर्ड पर यह सवाल दे सकती है
कुछ बच्चे इस सवाल को 30 + 5 के रूप में देखेंगे, जबकि कुछ अन्य बच्चे शायद इसे 20 + (9 + 1) + 5 में तब्दील कर लें। पहली कक्षा में खेले जाने वाले ‘दहाइयां’ और ‘ताश से दहाई’ जैसे खेलों से उनमें दहाइयों के रूप में सोचने की कुदरती प्रवृत्ति पुष्ट होती है।
बच्चों की सोच को समझने की कोशिश शिक्षक के लिए कठिन और थकाने वाली होती है। मगर यह काफी सुखदाई भी होती है क्योंकि जिन बच्चों को उन तरीकों से जोड़ने के लिए प्रेरित किया गया है, जो उन्हें ठीक लगते हैं, वे काफी ठोस बुनियाद पर खड़े होते हैं जहां से वे 33-15 और 8 x 23 जैसे सवालों को हल करने के अपने तरीके गढ़ने के लिए तैयार होते हैं।
कॉन्स्टेन्स कामी: बर्मिंघम स्थित अलाबामा विश्व-विद्यालय में अर्ली चाइल्डहुड एजुकेशन की प्रोफसर रही हैं। उन्होंने लगभग बारह साल तक पियाजे के अधीन पढ़ाई की।
लिण्डा जोसेफ: गणित पढ़ाती हैं।
अंग्रेज़ी से अनुवाद: सुशील जोशी: एकलव्य द्वारा प्रकाशित स्रोत फीचर सेवा से जुड़े हैं। विज्ञान लेखन में रुचि।
यह लेख लर्निंग नेटवर्क की पत्रिका रिवाइव के खंड-4, जनवरी 2006 से लिया गया है। मूल लेख नेशनल काउंसिल ऑफ टीचर्स ऑफ मेथेमेटिक्स द्वारा 1988 में प्रकाशित पुस्तक टीचिंग चिल्ड्रन मेथेमेटिक्स में छपा था।